(Königsberg preview) 

mercoledì 23 maggio 2012 ore 18,30

lettura di Alice Keller ore 19

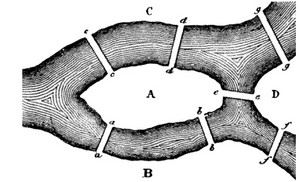
Eulero scrive: “A Königsberg in Prussia c’è un'isola A, chiamata der Kneiphof, e il fiume che la circonda si divide in due rami, come si può vedere in figura; i rami di questo fiume sono muniti di sette ponti a, b, c, d, e, f, g. Circa questi ponti veniva posta questa domanda, si chiedeva se fosse possibile costruire un percorso in modo da transitare attraverso ciascun ponte una e una sola volta. E mi fu detto che alcuni negavano ed altri dubitavano che ciò si potesse fare, ma nessuno lo dava per certo. Da ciò io ho tratto questo problema generale: qualunque sia la configurazione e la distribuzione in rami del fiume e qualunque sia il numero dei ponti, si può scoprire se è possibile passare per ogni ponte una ed una sola volta?”

Attraverso una dimostrazione discorsiva, effettuata con il solo ausilio delle lettere maiuscole assegnate alle regioni (ABCD), egli riuscì ad individuare una formula che consentiva, di stabilire se il cammino semplice era possibile oppure no. Riportiamo qui di seguito l'enunciato della soluzione che riguarda questo caso:

“Se sono più di due le regioni alle quali conducono un numero dispari di ponti, allora si può affermare con certezza che la passeggiata è impossibile”.

L’evento si propone come anteprima della mostra personale che Lucia Lamberti inaugurerà a Lipsia, presso la Salve Art Gallery, nell’ambito della settimana di festeggiamenti per il cinquantesimo anno di gemellaggio fra le città di Lipsia e Bologna.

[issuu width=420 height=149 backgroundColor=%23222222 documentId=120605060732-f95df15c53c14c49a4a70bb0221ff73e name=kon username=farnespazio tag=euler unit=px v=2]